
菜 单关 闭
一、引 言
球阀由于具有流体阻力小、操作方便、启闭迅速、密封性好和可靠性高等优点,在石油化工特别是煤化工行业得到广泛的应用。而煤化工原料因含有腐蚀性介质、硬物颗粒等,所以需要采用耐高压、耐腐蚀、耐磨损、适合温度范围广的金属硬密封球阀,此类球阀是通过预紧力和流体压力的双重作用,使球体与阀座压紧来实现密封。由机械设计及材料强度的相关理论可知,硬密封固定球球阀的主要失效形式为在保证阀体、球体、阀座、阀杆等不发生塑性变形的基础上发生泄漏,因此有必要预先了解此类球阀的密封副密封原理,从而对其进行深入探讨。图1为球阀整体半剖模型,图2为图1中红框内局部放大视图。当球体转动90°后使阀门处于关闭状态时,以密封环、O型圈为界将流体截断,此时阀座(进口端)受到弹簧预紧力F、流体压力P及球体对阀座作用力共同作用,由于F与G的左向合力大于右向合力(图2中水平方向白色箭头为作用力所对应区域),所以右向力需要球体对阀座作用力来抵消,此力所提供的压力即为密封比压,若密封比压大于密封必需比压,则不会泄漏。
图1 球阀整体半剖模型
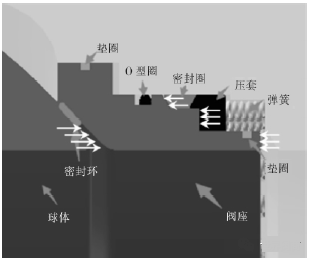
图2 密封副局部放大视图
2 密封性能分析及优化
2.1 模型主要尺寸
涉及本次分析模型的主要尺寸有:球阀总长:1276mm;阀体最小壁厚:156mm;球体半径:260mm;进口、出口、球体及阀座内径315mm;阀座最小外径:332mm;阀座全长:89mm;上阀杆直径:130mm;压盖外径:220mm;压盖最小壁厚:32mm;下阀杆直径:100mm。
2.2 模型简化策略
本文在对各零部件赋予同一材料属性(材料名称:ASTMA182F304镍合金,弹性模量:195GPa,泊松比:0.29,屈服强度:215MPa)进行了初步试算。试算时对阀体两端法兰处施加固定约束,上下阀杆施加轴向约束,对通过螺栓连接和过盈配合的接触对设置为绑定接触,阀座和垫圈也采用绑定接触,忽略O型密封圈,对其它可能会产生相对滑动的接触对设置为有摩擦接触,其摩擦系数设置为0.15。根据应力及变形分布的特点制定球阀有限元分析模型简化策略为:
1)因阀体刚度很大,变形量甚微,省略阀体。
2)球体上下方向是由上下阀杆做支撑,并无流体在该方向的作用,所以此方向上下阀杆的支撑作用也可视为无穷大,省略上阀杆,做轴向固定。
3)球体进出口方向分别由压盖和下阀杆支撑,因其刚度足够大到流体作用后变形量忽略的程度,所以该方向压盖和下阀杆的支撑作用也视为无穷大,省略压盖和下阀杆,做进出口方向的轴向固定。
4)O型圈、垫圈对球体与阀座的接触无影响,故建模时将O型圈及垫圈的凹槽填平,并省略O型圈、垫圈。
5)因是固定球阀,所以做对称即可,即最终由1/8球体和1/4阀座组成。
简化后的模型及相关尺寸如图3所示。
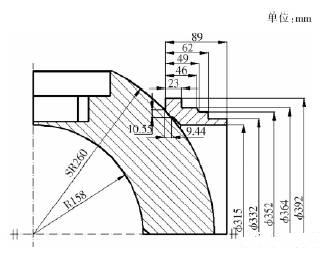
图3 简化模型相关尺寸图
2.3 边界条件
边界条件的施加如图4所示,图中A(斜线部分)为压盖对球体的限制作用,设为沿Z轴固定约束;B(“#”线部分)为上阀杆对球体的限制作用,设为沿X轴固定约束;C(颜色加深部分)处为阀体对阀座起径向限制作用,设为径向固定约束;在各个剖切面施加对称约束。
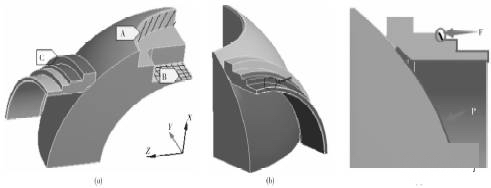
图4 边界条件示意图
阀座与球体之间设为不锈钢-不锈钢接触对,为了有效模拟实际接触情况,设置为非对称条件的有摩擦接触,因密封面加工精度高、表面粗糙度小,故摩擦系数取0.15。
由美标与国标换算关系可知流体施加压力P=(1500×2+1500/2)×0.00689=26MPa,其作用位置如图4b、图4c所示(颜色加深部分);设弹簧预压缩量6mm,弹性系数63N/mm,数量40个,则1/4阀座所受弹簧预紧力F=40×63×6/4N=3740N,其作用位置如图4c所示,即图4c圆圈位置既受到F同时也受到P的作用。流体压力P与弹簧预紧力F分2个时步进行加载,第一个时步加载F,第二个时步加载P,同时保持F不变。
2.4 网格无关性验证
有限元分析中网格的疏密程度对求解精度有一定的影响,通常网格越密求解结果越精确,但计算量大,计算机的配置需求增高,同时求解时间冗长,因此在保证计算精度的前提下,寻求最佳网格尺寸,以缩短计算时长是有必要的。
按2.2节材料属性及边界条件进行设置,以最小网格尺寸为基准核算阀座相对变形量0.1%误差为求解目标,球体和接触面分别由网格尺寸16mm和4mm的1/2n递减进行自适应网格化分(n=0,1,2,3,4)。其结果见表1,由表1可知,第3组数据的误差已经小于0.1%,故基于计算时间的考虑,最终取球体单元尺寸4mm,接触面单元尺寸1mm,而阀座体积较小,计算机配置及运算时间影响不大,不做网格无关性验证,取1mm,划分结果为六面体为主导结构化网格,节点数3394370,单元数899007,网格质量0.827,划分结果如图5所示
表1 网格无关性验证比较表
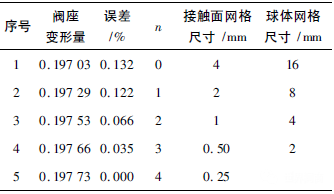

图5 网格划分结果
2.5 泄漏分析
图6、图7分别为球阀和球座的VonMises等效应力云图
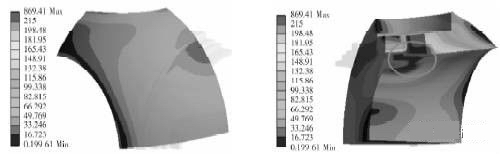
图6 球阀VonMises等效应力云图
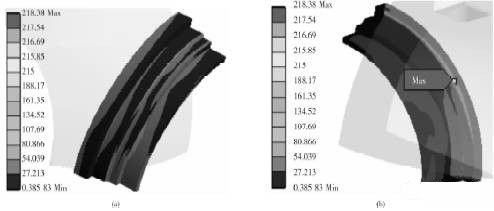
图7 阀座VonMises等效应力云图
图6中红色部分为VonMises等效应力高于球体材料屈服强度的区域。由图6a可知球体表面VonMises等效应力均低于屈服强度215MPa,基本不会发生塑性变形。图6b中出现了高于屈服强度的红色区域,主要分布在阀杆、压盖的安装孔根部周围,其主要原因为该处厚度较小刚度不足所造成的。可以预测图示红色区域,即VonMises等效应力超过屈服强度的部分将产生塑性变形,并最终导致球体表面的变形。此时引起的屈服变形可通过改变阀杆为花键连接或采用增加倒圆角的方式来改善。图7a中可见阀座基本不会发生屈服变形,即使图7b中最大处VonMises等效应力218.38MPa大于屈服强度215MPa,其原因是阀座内侧受到流体高压力而导致阀座变形,使其外侧与球体发生线面接触导致的。因本文重点研究密封性能,所以此处的改良不再深入分析优化。
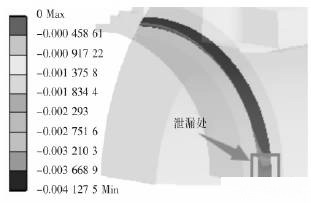
图8 开口度云图
图8中红框内标示的即为分离区域,该区域的贯通将导致密封环面开口而产生宏观的泄漏,提取密封环面上各个节点的变形值,取最小开口截面绘制其截面形状,图9实线为1/4环面所对应最小截面形状图(因开口高度数值较小,故对其进行放大100倍进行绘制),由离散点拟合曲线为二次多项式所示(图9虚线,R2=0.9986),因贯通开口为对称结构,利用拟合公式积分可计算出整个贯通开口截面积为0.1174mm2。
进一步计算可以得到阀门通过开口的泄漏量,必须说明的是该泄漏量并不包括因为密封比压不足而产生的渗透泄漏。应用孔口流量公式得密封环面泄漏流量为:
图8中红框内标示的即为分离区域,该区域的贯通将导致密封环面开口而产生宏观的泄漏,提取密封环面上各个节点的变形值,取最小开口截面绘制其截面形状,图9实线为1/4环面所对应最小截面形状图(因开口高度数值较小,故对其进行放大100倍进行绘制),由离散点拟合曲线为二次多项式所示(图9虚线,R2=0.9986),因贯通开口为对称结构,利用拟合公式积分可计算出整个贯通开口截面积为0.1174mm2。
进一步计算可以得到阀门通过开口的泄漏量,必须说明的是该泄漏量并不包括因为密封比压不足而产生的渗透泄漏。应用孔口流量公式得密封环面泄漏流量为:
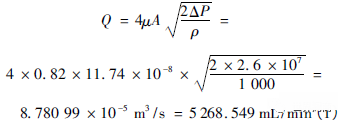
其中:Q为泄漏流量,单位m3/s;μ为流阻系数,取0.82;A为通流截面积,单位m2;ΔP为孔口两侧压强差,单位Pa;ρ为介质密度,单位kg/m3。
2.6 响应面设计及分析
采用DOE(DesignofExperiments)试验设计法以球体弹性模量、弹簧预紧力、球体半径、阀座相关尺寸L1、L2、L3为影响因素(如图10),以密封环面开口度为目标响应做了45组试验,从而找出众多因素中重要影响因素,以期为优化分析奠定基础。
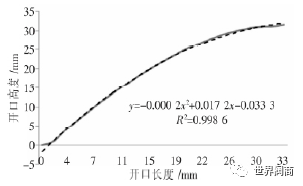
图9 密封环面最小开口处截面形状
图11为在DOE的基础上利用响应面设计所得各因素对密封环面开口度的敏感度变化趋势图,由图中可知,对密封环面开口度影响较大的4个因素由大到小依次为:L1、球体半径、弹性模量及L3,因此只需对上述参数进行合理筛选、组合设计,应能得到理想结果。
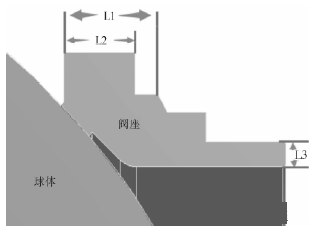
图10 优化控制变量示意图
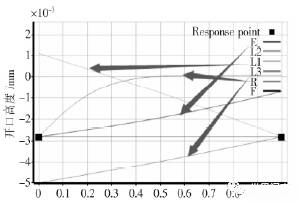
图11 敏感度变化趋势图
2.7 优选优化
经2.5节分析可知,影响密封环面开口度最大的因素为L1,即随着L1的减小可在一定程度上防止阀门泄漏问题。同时,为了减少加工工作量及不更换材料为目的,本文试着仅减小L1至36mm来进一步考查泄漏问题。
(1)密封必需比压。
对钢、硬质合金密封副,密封必需比压为:
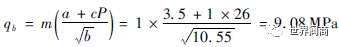
其中:qb为密封必需比压,单位MPa,m为介质系数,常温1,高温1.4;a、c为与密封面材料有关的系数,对于钢、硬质合金a取3.5,c取1;P为介质压力,单位MPa;b为密封在垂直于流体流动方向上的投影宽度,单位mm。
(2)优化结果泄漏分析
模拟所得密封环面的开口度如图12所示,图12中标示的Max与Min分别为开口的最大最小值,而红色区域是开口度为0的区域,由图中可见红色区域并未被其他颜色中断。
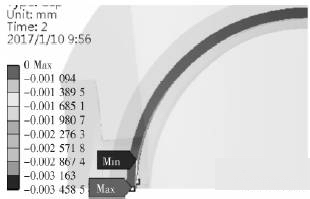
图12 开口度云图
图13为密封比压云图。由图13可知,密封面密封比压较大值主要分布在密封面外径处,并且越接近外径其值越大。在密封面外径附近的密封比压172.120MPa远远大于密封必需比压9.080MPa,故不存在密封泄漏问题。图13中红框内出现了浅蓝色区域,此区域有可能出现密封比压不足。对其进行径向线性压力分析,如图14,从图中可看出,密封比压最大值为17.739MPa,其大于密封必需比压9.080MPa,说明最有可能出现泄漏的区域也不会发生渗透泄漏。即使该阀门用于高压、高温场合(介质系数m=1.4),其密封必需比压12.715MPa也小于了密封比压17.739MPa。为了更可靠的密封性能要求可采用继续减小L1或减小阀座弹性模量(刚度)或增加球体半径来改善密封比压效果,在此不再多述
图13 密封比压云图
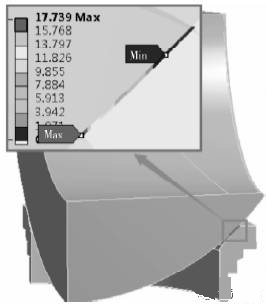
图14 最小密封比压线性压力云图

图15 阀座VonMises等效应力分布云图
由于L1的减小导致阀座刚度的降低,固阀座随着球体变形的随动作用更明显,但应力集中现象还会发生,同时也不难预测阀座的最大VonMises等效应力会有所下降,如图15,已小于屈服强度215MPa。
本次优化仅对L1做了变化,由2.5节分析可知L2的大小对密封性能是没有影响的,所以L2可作为调整L1的距离来改善阀座其它零件的协调安装(比如O型密封圈)。
3 结论
本文采用有限元方法,对硬密封球球阀在关闭状态下的静应力进行了分析。确定了1/8球体和1/4阀座为基本研究模型,在26MPa高压下的模拟结果为:阀杆、压盖安装孔根部周围将出现严重的应力集中现象,密封环面出现开口,开口最高处已达0.0041275mm,贯通开口截面积0.1174mm2,宏观贯通泄漏流量5268.594mL/min。
为了解决阀门泄漏问题,本文首先通过DOE试验设计及响应曲面分析法确定了对密封环面开口度影响较大的4个因素,然后对密封环面开口度影响最大的L1做了单因素优化仿真试验,结果表明:密封环面已不存在宏观贯穿开口,密封环面密封比压最小值也大于密封必需比压,泄漏问题已解决

扫一扫产品询价